A、ka1
B、ka2
C、

D、
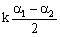
【正确答案】:D
【题目解析】:
【答案解析】本题考查方程组的解得表示,因为A为3阶矩阵,r(A)=2,因此方程组Ax=0的解空间的维数为:3-2=1,而 ,
, 为齐次线性方程组Ax=0的两个不同的解,因此一定有
为齐次线性方程组Ax=0的两个不同的解,因此一定有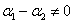 ,故可得Ax=0的通解为
,故可得Ax=0的通解为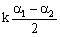 ,因此选择D,参见教材P112.(2014年4月真题)
,因此选择D,参见教材P112.(2014年4月真题)

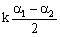
【答案解析】本题考查方程组的解得表示,因为A为3阶矩阵,r(A)=2,因此方程组Ax=0的解空间的维数为:3-2=1,而 ,
, 为齐次线性方程组Ax=0的两个不同的解,因此一定有
为齐次线性方程组Ax=0的两个不同的解,因此一定有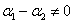 ,故可得Ax=0的通解为
,故可得Ax=0的通解为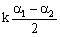 ,因此选择D,参见教材P112.(2014年4月真题)
,因此选择D,参见教材P112.(2014年4月真题)
📱 扫码体验刷题小程序

扫一扫使用我们的微信小程序