设二维随机变量(X,Y)的概率密度为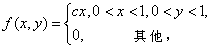 (1)求常数c;(2)求(X,Y)分别关于X,Y的边缘概率密度;(3)试问X与Y是否相互独立,为什么?
(1)求常数c;(2)求(X,Y)分别关于X,Y的边缘概率密度;(3)试问X与Y是否相互独立,为什么?
【正确答案】:
(1)由概率密度的性质 1= ,所以c=2。(2)由二维连续性随机变量边缘分布的定义
,所以c=2。(2)由二维连续性随机变量边缘分布的定义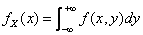 =
=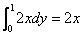 ,所以
,所以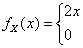
 ;
; ,所以
,所以
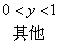 。(3)根据X与Y相互独立的充要条件是
。(3)根据X与Y相互独立的充要条件是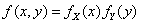 ,
, 
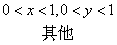 =
= ,所以,X与Y是相互独立的。
,所以,X与Y是相互独立的。
设二维随机变量(X,Y)的概率密度为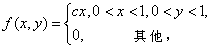 (1)求常数c;(2)求(X,Y)分别关于X,Y的边缘概率密度;(3)试问X与Y是否相互独立,为什么?
(1)求常数c;(2)求(X,Y)分别关于X,Y的边缘概率密度;(3)试问X与Y是否相互独立,为什么?
(1)由概率密度的性质 1= ,所以c=2。(2)由二维连续性随机变量边缘分布的定义
,所以c=2。(2)由二维连续性随机变量边缘分布的定义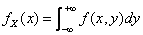 =
=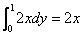 ,所以
,所以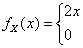
 ;
; ,所以
,所以
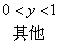 。(3)根据X与Y相互独立的充要条件是
。(3)根据X与Y相互独立的充要条件是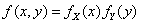 ,
, 
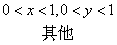 =
= ,所以,X与Y是相互独立的。
,所以,X与Y是相互独立的。
📱 扫码体验刷题小程序

扫一扫使用我们的微信小程序