【正确答案】:齐次线性方程组Ax=0只有零解
【题目解析】:
已知A为m×n实矩阵,则AT为n×m实矩阵,ATA为n×n正定矩阵,所以秩(ATA)=n。由矩阵秩的性质,秩A=秩AT,不妨设秩A=秩AT=r,存在非奇异矩阵Q,使得QAT= ,存在非奇异矩阵R,使得AR=(Cm×r 0),所以QATAR=
,存在非奇异矩阵R,使得AR=(Cm×r 0),所以QATAR=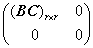 ,即秩(ATA)=r=n, 所以,齐次线性方程组Ax=0只有零解。
,即秩(ATA)=r=n, 所以,齐次线性方程组Ax=0只有零解。
已知A为m×n实矩阵,则AT为n×m实矩阵,ATA为n×n正定矩阵,所以秩(ATA)=n。由矩阵秩的性质,秩A=秩AT,不妨设秩A=秩AT=r,存在非奇异矩阵Q,使得QAT= ,存在非奇异矩阵R,使得AR=(Cm×r 0),所以QATAR=
,存在非奇异矩阵R,使得AR=(Cm×r 0),所以QATAR=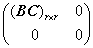 ,即秩(ATA)=r=n, 所以,齐次线性方程组Ax=0只有零解。
,即秩(ATA)=r=n, 所以,齐次线性方程组Ax=0只有零解。
📱 扫码体验刷题小程序

扫一扫使用我们的微信小程序