求线性方程组 .
.
【正确答案】:原方程组的通解为η=η*+k1ξ1+k2ξ2,其中k1,k2为任意常数.
【题目解析】:
构造增广矩阵并进行初等行变换 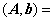
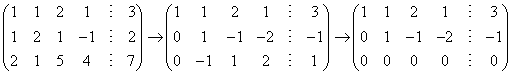
 =(T,d) 据此得到原方程组的同解方程组
=(T,d) 据此得到原方程组的同解方程组  取x3=x4=0得到一个特解
取x3=x4=0得到一个特解 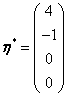 原方程组的导出组的同解方程组为
原方程组的导出组的同解方程组为 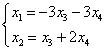 分别令
分别令 =
=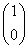 和
和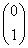 ,可求得基础解系
,可求得基础解系  ,
, , 于是求得原方程组的通解为η=η*+k1ξ1+k2ξ2,其中k1,k2为任意常数.
, 于是求得原方程组的通解为η=η*+k1ξ1+k2ξ2,其中k1,k2为任意常数.
求线性方程组 .
.
构造增广矩阵并进行初等行变换 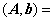
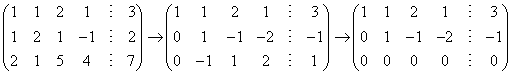
 =(T,d) 据此得到原方程组的同解方程组
=(T,d) 据此得到原方程组的同解方程组  取x3=x4=0得到一个特解
取x3=x4=0得到一个特解 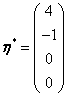 原方程组的导出组的同解方程组为
原方程组的导出组的同解方程组为 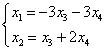 分别令
分别令 =
=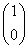 和
和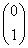 ,可求得基础解系
,可求得基础解系  ,
, , 于是求得原方程组的通解为η=η*+k1ξ1+k2ξ2,其中k1,k2为任意常数.
, 于是求得原方程组的通解为η=η*+k1ξ1+k2ξ2,其中k1,k2为任意常数.
📱 扫码体验刷题小程序

扫一扫使用我们的微信小程序