设 是四维向量,且线性无关,证明:
是四维向量,且线性无关,证明: 线性相关。
线性相关。
【正确答案】:
设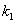 ,
,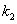 ,
, ,
, 为一组实数,且令
为一组实数,且令  0即
0即 =
= =0因为
=0因为 线性无关,所以
线性无关,所以 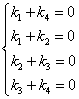 (*)而
(*)而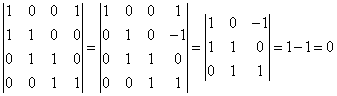 所以,方程组(*)有非零解,即
所以,方程组(*)有非零解,即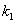 ,
,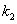 ,
, ,
, 为一组不全为零的常数,所以,向量组
为一组不全为零的常数,所以,向量组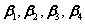 线性相关。
线性相关。
【题目解析】:
设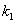 ,
,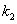 ,
, ,
, 为一组实数,且令
为一组实数,且令  0即
0即 =
= =0因为
=0因为 线性无关,所以
线性无关,所以 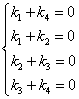 (*)而
(*)而 所以,方程组(*)有非零解,即
所以,方程组(*)有非零解,即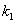 ,
,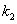 ,
, ,
, 为一组不全为零的常数,所以,向量组
为一组不全为零的常数,所以,向量组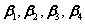 线性相关。
线性相关。
设 是四维向量,且线性无关,证明:
是四维向量,且线性无关,证明: 线性相关。
线性相关。
设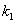 ,
,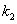 ,
, ,
, 为一组实数,且令
为一组实数,且令  0即
0即 =
= =0因为
=0因为 线性无关,所以
线性无关,所以 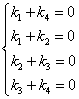 (*)而
(*)而 所以,方程组(*)有非零解,即
所以,方程组(*)有非零解,即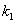 ,
,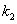 ,
, ,
, 为一组不全为零的常数,所以,向量组
为一组不全为零的常数,所以,向量组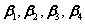 线性相关。
线性相关。
设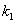 ,
,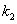 ,
, ,
, 为一组实数,且令
为一组实数,且令  0即
0即 =
= =0因为
=0因为 线性无关,所以
线性无关,所以 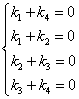 (*)而
(*)而 所以,方程组(*)有非零解,即
所以,方程组(*)有非零解,即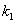 ,
,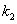 ,
, ,
, 为一组不全为零的常数,所以,向量组
为一组不全为零的常数,所以,向量组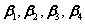 线性相关。
线性相关。
📱 扫码体验刷题小程序

扫一扫使用我们的微信小程序