【正确答案】:
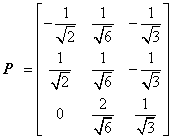 经正交变换x=Py后,原二次型化为标准形
经正交变换x=Py后,原二次型化为标准形 .
.【题目解析】:
本题考查实对称矩阵的相似标准形.给出二次型的矩阵形式f(x1,x2,x3)=xTAx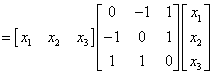 ,求A的特征值.
,求A的特征值.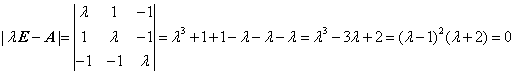 ,A的3个特征值为λ1=λ2=1,λ3=-2.属于λ1=λ2=1的特征向量满足
,A的3个特征值为λ1=λ2=1,λ3=-2.属于λ1=λ2=1的特征向量满足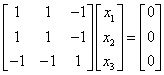 ,解得
,解得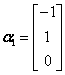 ,
,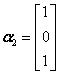 ,属于λ3=-2的特征向量满足
,属于λ3=-2的特征向量满足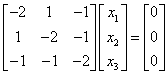 ,解得
,解得 .施密特正交化特征向量并单位化
.施密特正交化特征向量并单位化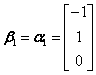 ,单位化
,单位化 ,
,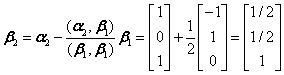 ,单位化
,单位化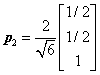 ,
,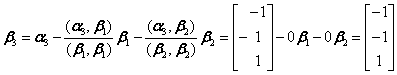 ,单位化
,单位化 ,得到正交矩阵
,得到正交矩阵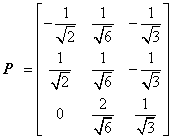 ,经正交变换x=Py后,原二次型化为标准形
,经正交变换x=Py后,原二次型化为标准形 .参见教材P154. (2013年1月真题)
.参见教材P154. (2013年1月真题)
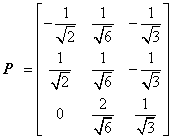 经正交变换x=Py后,原二次型化为标准形
经正交变换x=Py后,原二次型化为标准形 .
.本题考查实对称矩阵的相似标准形.给出二次型的矩阵形式f(x1,x2,x3)=xTAx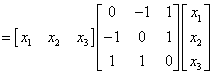 ,求A的特征值.
,求A的特征值.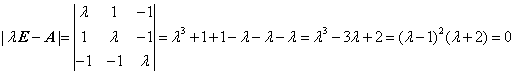 ,A的3个特征值为λ1=λ2=1,λ3=-2.属于λ1=λ2=1的特征向量满足
,A的3个特征值为λ1=λ2=1,λ3=-2.属于λ1=λ2=1的特征向量满足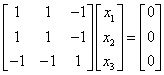 ,解得
,解得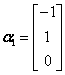 ,
,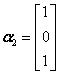 ,属于λ3=-2的特征向量满足
,属于λ3=-2的特征向量满足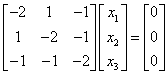 ,解得
,解得 .施密特正交化特征向量并单位化
.施密特正交化特征向量并单位化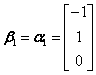 ,单位化
,单位化 ,
,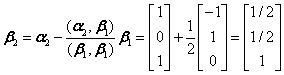 ,单位化
,单位化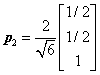 ,
,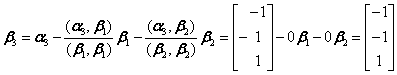 ,单位化
,单位化 ,得到正交矩阵
,得到正交矩阵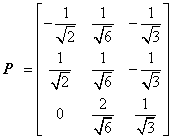 ,经正交变换x=Py后,原二次型化为标准形
,经正交变换x=Py后,原二次型化为标准形 .参见教材P154. (2013年1月真题)
.参见教材P154. (2013年1月真题)
📱 扫码体验刷题小程序

扫一扫使用我们的微信小程序