设四元方程组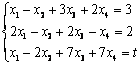
，问t取何值时该方程组有解？并在有解时求其通解.
【正确答案】：
， 
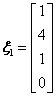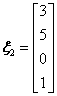，原方程组的通解β＝η*＋k1ξ1＋k2ξ2，其中 k1,k2为任意常数.【题目解析】：
本题考查非齐次线性方程组的求通解方法.构造方程组的增广矩阵并施行初等行变换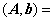 
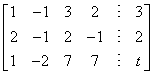
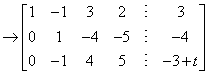
， 所以 
时，
，方程组有解.求解如下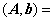 
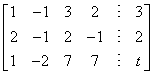
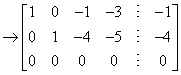
据此得到原方程组的同解方程组
取x3＝x4＝0得到一个特解， 原方程组的导出组的同解方程组为
， 分别令
和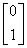
，可求得基础解系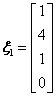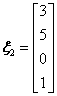， ，原方程组的通解β＝η*＋k1ξ1＋k2ξ2，其中 k1,k2为任意常数. 参见教材P120. （2013年1月真题）
