设A=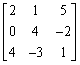 ,B是三阶方阵,且满足AB-A2=B-E,求B.
,B是三阶方阵,且满足AB-A2=B-E,求B.
【正确答案】:
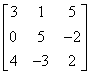
【题目解析】:
本题考查方阵的逆矩阵.AB-A2=B-E,AB-B=A2-E,(A-E)B=A2-E,因为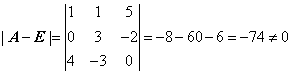 所以A-E可逆,原方程有解;根据|A-E|=-74、三阶矩阵A-E的元素情况及逆矩阵的定义可知,宜采用行列式方法求其逆矩阵,计算如下A11=-6,A12=-8,A13=-12,A21=-15,A22=-20,A23=7A31=-17,A32=2,A33=3得
所以A-E可逆,原方程有解;根据|A-E|=-74、三阶矩阵A-E的元素情况及逆矩阵的定义可知,宜采用行列式方法求其逆矩阵,计算如下A11=-6,A12=-8,A13=-12,A21=-15,A22=-20,A23=7A31=-17,A32=2,A33=3得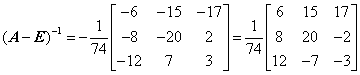 ,而
,而 ,
,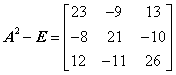 ,所以
,所以
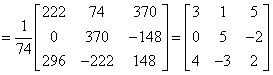 .参见教材P48. (2013年1月真题)
.参见教材P48. (2013年1月真题)
