已知4元线性方程组 ,(1)确定a的值,使方程组有解;(2)在有解时,求出其通解(要求用它的一个特解和导出组的基础解系表示).
,(1)确定a的值,使方程组有解;(2)在有解时,求出其通解(要求用它的一个特解和导出组的基础解系表示).
【正确答案】:
(1)当6a+1=0,即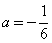 时,方程组有解.(2)
时,方程组有解.(2) ,
, ,原方程组的通解为
,原方程组的通解为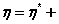 k
k ,其中k为任意常数.
,其中k为任意常数.
【题目解析】:
本题考查非齐次线性方程组的求通解方法.先把增广矩阵化简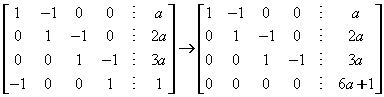 (1)当
(1)当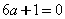 ,即
,即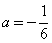 时,方程组有解.(2)将
时,方程组有解.(2)将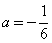 代入增广矩阵,得
代入增广矩阵,得 ,据此得到原方程组的同解方程组
,据此得到原方程组的同解方程组 ,得方程组的一个特解
,得方程组的一个特解 ,原方程组的导出组的同解方程组为
,原方程组的导出组的同解方程组为 取
取 ,得基础解系
,得基础解系 于是原方程组的通解为
于是原方程组的通解为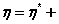 k
k ,其中k为任意常数. 参见教材P120. (2013年4月真题)
,其中k为任意常数. 参见教材P120. (2013年4月真题)
