已知矩阵A=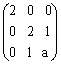 的一个特征值为1,求数a,并求正交矩阵Q和对角矩阵
的一个特征值为1,求数a,并求正交矩阵Q和对角矩阵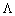 ,使得Q-1AQ=
,使得Q-1AQ=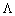 .
.
【正确答案】:
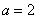 ,
,
【题目解析】:
特征方程为: 因为它的一个特征值是1,因此可得1是
因为它的一个特征值是1,因此可得1是 的解,代入
的解,代入 可得
可得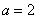 ,因此特征方程为:
,因此特征方程为: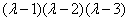 ,故可得特征值为1,2,3,当
,故可得特征值为1,2,3,当 时,对应的齐次方程组为
时,对应的齐次方程组为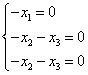 ,因此可得解为
,因此可得解为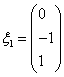 当
当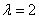 时,对应的齐次方程组为
时,对应的齐次方程组为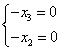 ,因此可得解为
,因此可得解为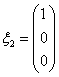 当
当 时,对应的齐次方程组为
时,对应的齐次方程组为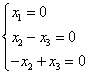 ,因此可得解为
,因此可得解为 这三个解是正交的,将它们单位化可得
这三个解是正交的,将它们单位化可得 ,
, ,
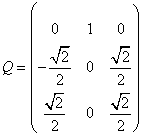
,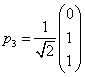 因此可得矩阵Q为:
因此可得矩阵Q为: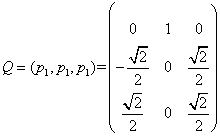 ,参见教材P154.(2014年4月真题)
,参见教材P154.(2014年4月真题)
已知矩阵A= 的一个特征值为1,求数a,并求正交矩阵Q和对角矩阵
的一个特征值为1,求数a,并求正交矩阵Q和对角矩阵 ,使得Q-1AQ=
,使得Q-1AQ=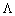 .
.
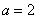 ,
,
特征方程为: 因为它的一个特征值是1,因此可得1是
因为它的一个特征值是1,因此可得1是 的解,代入
的解,代入 可得
可得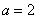 ,因此特征方程为:
,因此特征方程为: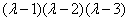 ,故可得特征值为1,2,3,当
,故可得特征值为1,2,3,当 时,对应的齐次方程组为
时,对应的齐次方程组为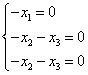 ,因此可得解为
,因此可得解为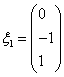 当
当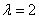 时,对应的齐次方程组为
时,对应的齐次方程组为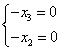 ,因此可得解为
,因此可得解为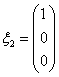 当
当 时,对应的齐次方程组为
时,对应的齐次方程组为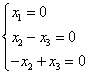 ,因此可得解为
,因此可得解为 这三个解是正交的,将它们单位化可得
这三个解是正交的,将它们单位化可得 ,
, ,
,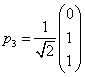 因此可得矩阵Q为:
因此可得矩阵Q为: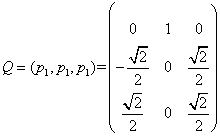 ,参见教材P154.(2014年4月真题)
,参见教材P154.(2014年4月真题)
📱 扫码体验刷题小程序

扫一扫使用我们的微信小程序