设函数f(x)在 上连续,在(1,2)内可导,且f(2)=0,F(x)=(x-1)f(x),证明:至少存在一点
上连续,在(1,2)内可导,且f(2)=0,F(x)=(x-1)f(x),证明:至少存在一点
 (1,2),使得
(1,2),使得 (
(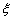 )=0.
)=0.
【正确答案】:
由已知:f(x)在 上连续,在(1,2)内可导,且f(2)=0,可得:F(x)在
上连续,在(1,2)内可导,且f(2)=0,可得:F(x)在 上连续;在(1,2)内可导;且F(1)=0, F(2)= f(2)=0,所以由罗尔定理:至少存在一点
上连续;在(1,2)内可导;且F(1)=0, F(2)= f(2)=0,所以由罗尔定理:至少存在一点
 (1,2),使得
(1,2),使得 (
(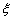 )=0.
)=0.
设函数f(x)在 上连续,在(1,2)内可导,且f(2)=0,F(x)=(x-1)f(x),证明:至少存在一点
上连续,在(1,2)内可导,且f(2)=0,F(x)=(x-1)f(x),证明:至少存在一点
 (1,2),使得
(1,2),使得 (
(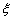 )=0.
)=0.
由已知:f(x)在 上连续,在(1,2)内可导,且f(2)=0,可得:F(x)在
上连续,在(1,2)内可导,且f(2)=0,可得:F(x)在 上连续;在(1,2)内可导;且F(1)=0, F(2)= f(2)=0,所以由罗尔定理:至少存在一点
上连续;在(1,2)内可导;且F(1)=0, F(2)= f(2)=0,所以由罗尔定理:至少存在一点
 (1,2),使得
(1,2),使得 (
(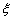 )=0.
)=0.
📱 扫码体验刷题小程序

扫一扫使用我们的微信小程序